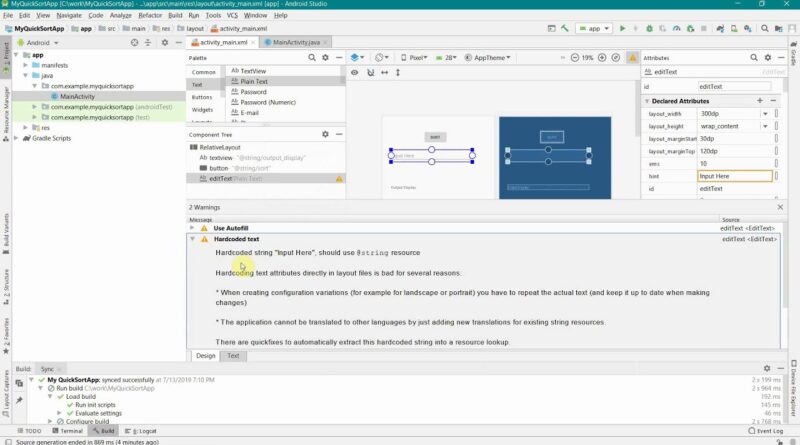
Methods to develop a Fast Kind recursive Algorithm App in Android Studio?

This video reveals the steps to implement or create a Fast Kind Android App utilizing Android Studio.

For Bubble Kind Tutorial please check with the under video:

We will likely be glad to listen to from you relating to any question, options or appreciations at: [email protected]

https://programmerworld.co/android/how-to-develop-a-quick-sort-recursive-algorithm-app-in-android-studio/

Supply Code:

bundle com.instance.myquicksortapp;

import android.assist.v7.app.AppCompatActivity;
import android.os.Bundle;
import android.view.View;
import android.widget.EditText;
import android.widget.TextView;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Checklist;

public class MainActivity extends AppCompatActivity {
non-public TextView textView;
non-public EditText editText;

@Override
protected void onCreate(Bundle savedInstanceState) {
tremendous.onCreate(savedInstanceState);
setContentView(R.structure.activity_main);

editText = findViewById(R.id.editText);
textView = findViewById(R.id.textview);
}

public void SortButton(View view){
String[] stringsNumber = editText.getText().toString().cut up(“,”);
Integer[] integersNumber = new Integer[stringsNumber.length];

for (int i = 0; i [LESS THAN] stringsNumber.size; i++){
integersNumber[i] = Integer.parseInt(stringsNumber[i]); //Changing from String Array to Integer Array
}
Integer[] sortedNumbers = QuickSort(integersNumber);
textView.setText(Arrays.toString(sortedNumbers));
}

non-public Integer[] QuickSort(Integer[] numbers){
int n = numbers.size;
if(n [LESS THAN] 2){
return numbers;
}

Integer[] sortedNumber = new Integer[n];
Checklist[ANGLED BRACKET]Integer[ANGLED BRACKET] leftNumbers = new ArrayList[ANGLED BRACKET]Integer[ANGLED BRACKET]();
Checklist[ANGLED BRACKET]Integer[ANGLED BRACKET] rightNumbers = new ArrayList[ANGLED BRACKET]Integer[ANGLED BRACKET]();

for(int i=0;i [LESS THAN] n-1;i++){
if ((numbers[i] [LESS THAN] numbers[n-1])){
leftNumbers.add(numbers[i]);
}else{
rightNumbers.add(numbers[i]);
}
}
Integer[] leftNumberSorted = QuickSort(leftNumbers.toArray(new Integer[leftNumbers.size()]));
Integer[] rightNumberSorted = QuickSort(rightNumbers.toArray(new Integer[rightNumbers.size()]));
int ok;
for (ok=0; ok [LESS THAN] leftNumberSorted.size;ok++){
sortedNumber[k]=leftNumberSorted[k];
}
sortedNumber[k] = numbers[n-1];

for (int j=0; j [LESS THAN] rightNumberSorted.size; j++){
sortedNumber[++k] = rightNumberSorted[j];
}
return sortedNumber;
}
}

source